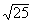Axioms of Equality and Order / Mathematics-Algebra

Fundamental Concepts of Intermediate Algebra

Topic:  Axioms of Equality and Order
           Property of Real numbers

1. Equality - symbol is " = " and read as " equals " or " is equal to ", a statements that symbol or group of symbols which represents an equal quantity.

sample:   a = a      " a is equal to a itself "    or " A quantity of a is equal to itself "

Properties of equality

The above example is an Reflexive Property of equality. Reflexive property is a quantity which reflect a it self, or a quantity which is exactly the same as it self.

example :                 Y + 7 = 7 + Y    ,     p + 1  + z  = 1 +  z  +  p    

Symmetric Property - it is where the first quantity is equal to the second quantity and reversible.

example :                  a = b      so     b = a

                      or  a + b = 7     so     b + a = 7

                      or  5 + c = 10   then  c + 5 = 10

Transitive Property - when the quantity of the first is equal to the quantity of the second and the second is equal to the quantity of the third, then the quantity of the third is equal to the quantity of the first.

example :             z = b , b = y then y = z

                   or     a + 4 = b , b + 4 = a     therefore  a = b

Substitution Property - it is when the two elements are having the same quantity or equal with each other so you can replace element one to another element, and vice versa..

example:           If  y - 5 = z   and y = a  ,  then    a  -  5 = z

Every real number are having its pair of only point and its point is having only one real number. That point is associated with a line, and that is called a Line number. 

Line number is helpful in knowing the relationship between numbers. And the number are called as coordinates of every points, and the points are the graphs of the numbers.

Transitive Property - it is always associated with a " greater than " or " > " and " less than " or " < ". When a first element is less that the second, and the second is less than the third, therefore the third is greater than the first.

example :           when    x < y ,  and y < z ,,  therefore  z  >  x.

Related Posts :

 

Intermediate algebra about Set, Venn diagram

Read More

Intermediate Algebra / Fundamental Concept

Intermediate Algebra - Mathematics

Mathematics: Fundamental Concepts of Algebra:

 Topics :  Set

Definition:    

1.      set - is a group or collection of objects. 
2.      elements or member - it is an object that is inside the set

Example of an Set :

                

               A =   {  2 , 4 , 6,  14  }        B =  {  3, 6, 9, 12  }      Z =  {  all members of math class }

the Sets name are employed to be  " A " ,  " B " and " Z "

      elements or members are inside this symbol "  {   }  " 

example are :    {  2 , 4 , 6,  14  }   ,,,,,  {  3, 6, 9, 12  }   ,,,,   {  all members of math class }

In doing such phrase  we will be using the symbol " " as " is an elements of " or " is a member of ". 

 We take a look on our sample :  A =  {  2 , 4 , 6,  14  }  from here we can write :

             4    A , to say that 4 is a member or elements of Set A

             2    A,  to say that 2 is a member or elements of Set A

We will be also using a symbol " " to represent of  " is not a member of " or " is not an element of "

       

Lets get same example on set A:              A =  {  2 , 4 , 6,  14  }  ,         B =  {  3, 6, 9, 12 }

        we can say that 4  B,,  or 4 is not a member or element of Set B 

                                 3  A ,, 3 is not a member or element of A

A set can be said to be equal if they are having the same elements,, 

                                        

         set a is = to set b            =====                    A =  {  2 , 4 , 6,  14  }  ,,,, B =  {  4, 6 , 2, 14 }

                                                                     or     A =  {  of math students  }  

                                                                             B =   {  students of math subject}

On some other matter, a set is containing an infinite numbers and we can't list all of those elements. We simple list numerous number which is sufficient enough to explain its pattern and we are adding such dots on series of this. 

Like example :

 A =  {  1, 2, 3, 4 , 5 .... }

 B =  {  2, 4, 6, 8, 10 ....... }

or

 C =  {  0 , 1 , 2 ...... }

The above numbers are said to be a set of counting or natural numbers. 

Sometimes the set is not containing an elements or members. This set is called a null or empty set. The symbol for this are " ø " or  "{   } ". 

sample of this are : { negative natural numbers }

Definition:

1.    subset - a subset means such set that contain a number or several numbers of elements on another set. 

Subset symbol:    " "

Sample of Subset :  Set A is a subset of Set B or " A  B "

                  A = "{ 1 , 4,  5   } "  and B = "{ 1, 2, 3, 4, 5, 6, 7 } "

Set A is a subset of Set B, or called as Proper subset

if   C = "{ 5, 1, 4  } " and will be " A  C ". So this kind of subset will be the Improper subset.

Definition:

1.         Union -  is a combination of two set elements. Symbol is " U "

Sample: A U B or set A is union of set B

 ex: 

         A = { 1, 2, 3, 4 , y , x } .    B = { 2, 4, 1, 3, a , b} 

then : A U B = {1 , 2, 3 ,4 , y, x, a, b} . 

Definition : 

1. Intersection - the elements or member which is common on the different sets. 

Symbol of intersection " ∩ "

sample:  if A = { 1, 2, 3, z, a  }, and B = { 1, , 4,  5,  a , y }  

So the A ∩ B = { 1 , a }

Venn Diagram

Venn Diagram is mostly being used in illustrating the relationship between sets. The color illustrate relation between the sets.

A U B 

A ∩ B

B is completely contained in set A

A ⊂ B

Definition : 

1.  Set of Integers - is the sets of natural numbers combined with their negative and zero.

sample : I = {.....-2,  -1, 0, 1 , 2 .....  }

     2. Set of rational numbers - a set of members or elements which can be express as a / b. Which is a and b are integers and b is not equal to zero.

      3. Set of irrational numbers - it is an elements which consists of decimal presentations and either 

non-repeating or non-terminating. 

sample: { -4, 0, 3.7,  , , , 10/3, 8, 1.010001001 }

      4. Set of real number - it is the union of rational and irrational numbers.

Read More